4种土壤入渗测定方法的比较

摘要：入渗是土壤的基本物理性状，与降雨产流、侵蚀、非点源污染等过程密切相关，快速、准确测定土壤入渗速率具有重要的意义。以黄土高原沟壑区安塞水土保持综合试验站大豆地的黄土为测试土壤，利用双环、单环、圆盘入渗仪、Hood入渗仪4种方法测定了土壤入渗性能，并以双环法测定的稳渗速率、Hood仪测定的饱和导水率、单环／双环和圆盘测定的累积入渗量为基础，比较分析了4种方法各自的优劣。结果表明，单环、圆盘、Hood测定的稳渗速率分别为双环的116%，111%和225%，双环、单环、圆盘测定的饱和导水率分别为Hood的65.8%，75.1%和105%，双环、单环、圆盘达到稳渗时间分别为100，80和30min。说明圆盘测得的稳渗速率、饱和导水率接近标准值，而且省时省力省水，更适合于野外实验。

        朱显漠先生曾在黄土高原国土整治“28字方略”中提到“全部降水就地入渗拦蓄”，而土壤渗透性影响“入渗拦蓄”过程。因此认识黄土高原的土壤入渗特征对于洪水预报和土壤侵蚀预测预报，以及对制定水土保持措施，均有十分重要的意义。

        目前测定土壤入渗速率的方法主要有注水法（如双环法）、水文法和人工降雨法，测定饱和导水率方法则很多，如定水头渗透仪法、变水头渗透仪法、盘式入渗仪法等。众多方法中，双环法被认为准确的方法，实际应用多。

       国内外许多研究均涉及了土壤入渗测定方法的比较，虽然双环法是田间测定土壤渗透性能常用、经典的方法，也是判断其他方法测定结果的基础，但双环法一般只是测定土壤表层入渗能力，而且耗水量大、耗时间长，为了保持双环内水头深度一致，当利用双环法测定坡地土壤入渗时，需要平整地表，这种扰动可能对测定结果影响很大，而土壤入渗速率主要取决于土壤表层的性状，双环安装时的地表扰动自然会对试验结果产生影响，且这种影响随着坡度的增大而增大。因此需要选择一种相对既省时省力又准确方便的方法来替代双环法进行坡面土壤入渗过程的测定。

1研究区概况与实验方法

1.1研究区概况

    中国科学院安塞水土保持综合试验站地处黄土高原腹地（109°19’23”E，36°51’30”N），属中温带大陆性半干旱季风气候区，年均气温8.8°C，年均降水量549mm，降水多以短历时暴雨为主，降雨在年内分布集中6-9月的降水量占到全年降水量的70%以上。实验在试验站平坦川地的大豆地内的无雨天连续进行，土壤为黄绵土，属于典型的粉壤土，砂粒含量为26.33%，粉粒含量为67.02%，黏粒含量为5.51%，土壤容重为1081kg/m3，有机质含量为0.9%。

   1.2实验方法

1.2.1 单环和双环法测定方法双环实验的内径35cm，外径50cm，高度均为18.5cm。在实验区选较为平坦的样地，去除地表作物，将圆环用橡胶锤缓慢均匀地打入土中12.5cm，尽量保持土壤结构不受破坏。利用直径为25cm的马氏瓶为圆环供水，当内环和外环中的水层厚度达到3cm时，开始用秒表记时，并分别在0.0，0.5，1，2，3，5，7，10，15，20，25和30min及之后每10min读取供水桶标尺刻度值，实验过程中保持内外环水面高度为3cm，读数时一并读取水温。单环实验用双环的内环来完成，实验过程与双环法相同。

1.2.2 圆盘入渗仪测定方法圆盘入渗仪为澳大利亚生产的CSIRO圆盘入渗仪（已停产）（discpermeameter），（SW080B张力土壤入渗仪可作为替代品，产品详情链接：http://dianjiangtech.cn/product/109-cn.html），由储水管、调压管和入渗盘组成。实验时选择平整样地，去除地表作物，同时在样地周围用环刀取样，测定土壤初始含水量及容重。将半径10cm、高3mm的钢环安置在测定点，环内铺满过0.25mm筛子的细沙，用钢尺刮平，并将钢环移走；用注射器调整恒压管中水位高度为20mm，将圆盘入渗仪放入水桶中，用抽气筒给储水管充满水后关闭阀门；取出入渗仪，轻拍入渗盘使其中的气泡溢出，擦干圆盘上的水；将圆盘放置于吸水物上，确保储水管没有气泡产生，记录储水管水位初始高度，将仪器小心放在测定点，使其与沙面紧密接触；当储水管中产生气泡时开始计时，前10次读数时间间隔为0.5min，随后5次读数间隔为2min，8次读数间隔为5min，最后读数间隔为10min，直至达到稳定入渗，读数时一并读取水温。实验结束后，移开入渗仪，立刻铲去部分沙层，取表层2～3mm土壤约30g，测定土壤含水量。

1.2.3 Hood入渗仪测定方法Hood入渗仪为德国UGT公司生产的Hood IL－2700型入渗仪，由Hood水罩（直径17.6cm或24.8cm）、U形管压力计、导水管路、储水管等组成。实验时尽量选择平整样地，去除地表作物，安置钢圈并部分压入土壤，将水罩放置在钢圈内，并在水罩和钢圈之间用过0.5mm筛子的饱和湿沙密封；给U形管注水，使液面平于0刻度线处；连接管路，关闭所有阀门，然后给内、外管注水，外管水面低于内管；配合阀门和调压管调节水罩中间水柱高度与U形管液面差，此二者之差即为水罩中施加于土壤表层的压力值，本实验调出0和4cm两个压差。开始计时，液面每下降5mm记录1次时间，直至观测值达到稳定，读数时一并读取水温。以上实验各进行3次，将3次实验数据平均，进行土壤稳渗速率、土壤饱和导水率的计算。

1.3数据处理方法

数据处理、制图分别采用Excel，SPSS和Origin等软件进行。其中，为了检验双环、单环、圆盘累积入渗量在变化趋势和数值方面的差异性，利用SPSS17.0软件，选取双环、单环、圆盘在10，15，20，30，40，50，60，70和80min时累积入渗量（mm）进行Pearson相关性分析和独立样本T检验。

2 土壤初渗速率、稳渗速率、饱和导水率的计算

2.1土壤初渗速率

由于初始观测阶段读数误差和系统误差无法估测，所以初始入渗速率ｆ_0（mm／min），计算公式为：

式中：q₀———入渗开始3min的实测累积入渗量（mm）；t₀———3min。

2.2 土壤稳渗速率

单环和双环法计算公式为：

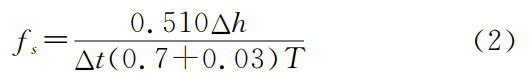
式中：fs———10℃标准水温时土壤入渗速率（mm／min）；Δh———某一时段Δt供水桶读数差值（mm）；Δt———时段（min）；T———某时段的平均水温（℃）。

圆盘入渗仪计算公式为：

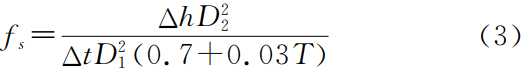
式中：D1———入渗盘的有效直径（cm）；D2———储水管直径（cm）。

Hood入渗仪计算公式为：

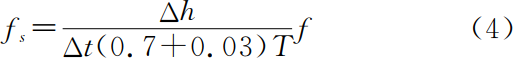
式中：ｆ———横切面面积指数，即储水管截面积与入渗面积之比，小Hood罩为0.313，大Hood罩为0.156。

2.3 土壤饱和导水率

土壤导水率Ks与压力h间的关系可以用GarD－ner指数函数描述：

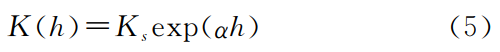
式中：K（h）———给定压力下的导水率（mm／min）；Ks———饱和导水率（mm／min）；a———为与土壤结构和毛管吸力有关的因子；h———压力值（cm）。

WooDing研究发现稳态入渗量（Q，cm3／min）与圆形入渗面（半径为r，cm）的关系为：

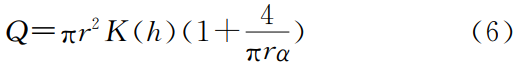
式中：Q——可由累积入渗水量（cm3）与累积时间（min）做回归曲线求得，曲线线性部分的斜率即为稳态入渗水量（cm3／min）。将（5）式代入（6）式得：

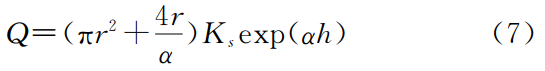
公式（7）为圆盘入渗仪饱和导水率计算公式。而对于单环／双环法其饱和导水率由公式（8）计算：

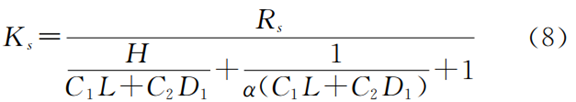
式中：H———水头高度（cm）；L———内环入土深度（cm）；D1———内径（cm）；C1，C2———无量纲经验常量，其值分别为0.316π和0.184π。Parlang发现公式（5）中的a满足a＝a（h），PhiliP研究指出在多数情况下令a为常数，仍能有效地表达K（h），因此对于单环／双环法，令a＝0.2cm－1，即可利用公式（8）进行计算。

对公式（7）两边取对数：

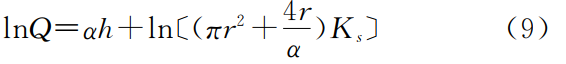
公式（9）为Hood入渗仪饱和导水率的计算公式，式中lnQ与h呈线性关系，其中a用公式（10）计算：

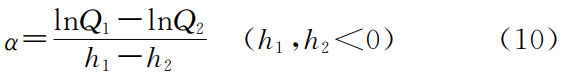
3 结果与讨论

3.1入渗性能比较分析

对4种不同方法测定土壤入渗量进行计算分析，得到入渗性能比较（表1），同时根据过程点数据利用Origin软件绘制入渗过程图（图1）。

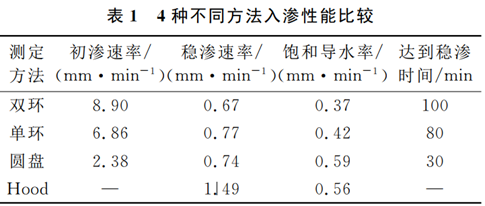
       由表1可以看出，不同方法测定的初渗速率、稳渗速率、饱和导水率和达到稳定的时间，均存在显著差异。

      就初渗速率而言，双环、单环、圆盘存在较大差异，可能是由于圆盘接触面积小且与土表间有干沙层、单环／双环环壁与土体之间缝隙等导致的。

      稳渗速率是反映土壤渗透性能的主要指标，也是判断不同土壤、不同土地利用条件下土壤入渗性能差异的基础，对其准确测量具有重要的意义。从表1可知，与双环法测定结果相比，单环由于存在明显的侧渗现象，稳渗速率偏大，为双环测定结果的116%，这与Wu等的研究结果一致；与单环法类似，圆盘入渗仪也存在一定侧渗，稳渗速率也较双环法为大，平均稳渗速率为双环的111%，这与许明祥等人的研究结果相反，造成这种差异的原因可能在于土壤性质的时空变异及计算公式的不同；用Hood仪法测定土壤入渗时存在很大的侧渗现象，从而导致Hood入渗仪测定的稳渗速率为双环的225%。

      饱和导水率是土壤渗透性能的另一种量化表述，在土壤物理学、坡面水文过程及侵蚀过程模拟中应用非常为广泛。由表1可知，由于单环／双环、圆盘法均使用了经 验参数参与计算，而Hood仪法均使用实测值，所以以Hood仪值为标准，双环测值为Hood的65.8%，这与BoDhinayaKe的研究结果一致；单环测值为Hood的75.1%；圆盘测值为Hood的105%。

     实验耗时是野外实验需要考虑的比较重要的因素，由表1可知达到稳定入渗的时间上双环约为100min，单环约为80min，圆盘约为30min，而Hood仪考虑调压过程总时间约为30min。综合来看，圆盘入渗仪法在稳渗速率和饱和导水率上均靠近标准值，而且用时短。

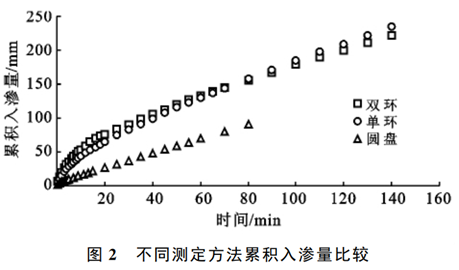
      由图1可以看出，入渗初期双环的入渗速率大于单环的入渗速率，但在25min前后开始小于单环，并持续到稳渗阶段，直到实验结束。实验初期（20min）土壤入渗速率较大且读数间隔短，供水桶水面波动增大了水位观测的随机误差，因此单环和双环的测定结果存在较大波动，且双环法波动性更大。与单环和双环入渗仪相比，圆盘入渗仪用水量很小，实验时间短，供水管水位变化相对比较稳定，测定结果一直比较稳定，但由于50min左右换盘的影响，导致入渗曲线略有上升趋势。

3.2累积入渗量对比分析

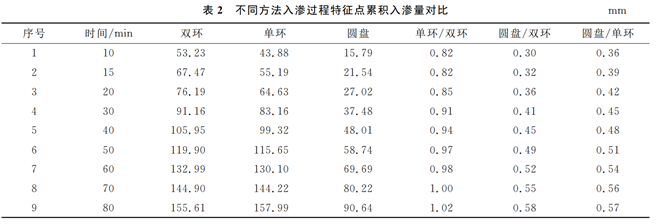
不同方法测定的累积入渗量均随着入渗时间的延长而增加（图2），但受入渗达到稳定时间（表1）的影响，不同方法间土壤累积入渗量与时间的关系曲线存在明显差异。前20min单环／双环增长速度较快，且双环大于单环，之后趋于平稳增长。在80min前后单环累积入渗量开始大于双环，且稳定后的单环增长率大于双环。由于圆盘入渗仪达到稳定的时间短，累积入渗量只在前5min内迅速的增加，而后基本保持平稳增长。表2给出了不同方法入渗过程特征点的累积入渗量，从表中可以看出随着时间的延长，单环与双环、圆盘与双环、圆盘与单环的比值逐渐增大，并有继续增大的趋势。

以不同方法入渗过程特征点累积入渗量（表2）为基础，进行相关性和差异性分析，发现双环、单环和圆盘的两两组合均具有很强的相关性。

对于T检验，“双环—单环”组合P值大于0.05，说明单环／双环差异性不显著，而“双环—圆盘”和“单环—圆盘”量种组合P值均小于0.05，则说明其中二者差异显著。

由此说明，3种方法测定的累积入渗量在趋势上具有很强相关性，而数值方面圆盘和单环、双环之间差异性显著，同时也从侧面说明了圆盘入渗仪适合在黄土丘陵区进行土壤入渗测定。

3.3 其他相关方面的比较分析

除了量化比较外，结合前人的相关研究成果和实验经验，列举了4种方法在用水量、实验耗时、对地表的扰动程度、实验误差、实验原理、入渗面积及有无侧渗等诸多方面的定性比较（表3）。从表3可以看出，圆盘入渗仪在上述诸多方面，都具有一定的优势，从而表明圆盘入渗仪在黄土高原土壤入渗测定中具有很强的优越性。

4 结论

利用实测土壤入渗数据，比较了双环法、单环法、圆盘法和Hood入渗仪测定的稳渗速率、累积入渗量的差异，结果发现圆盘法测定的稳渗速率为双环的111%，饱和导水率为Hood的105%，均接近标准值；单环／双环、圆盘3种方法测定的累积入渗量趋势上在99%置信区间内显著相关，单环和双环数据上差异不显著，而单环、双环与圆盘差异显著；圆盘法实验耗时平均约为30min，约为双环和单环法实验耗时的1／3，单位面积上实验用水仅为双环法的1／2左右；圆盘法不扰动表土，读数相对准确。综合比较4种测定方法，圆盘法具有省时、省力、省水、准确等优势，可以替代双环法进行坡面土壤渗透性的测定。

来源：朱良君，张光辉，任宗萍 4种土壤入渗测定方法的比较【水土保持通报 第32卷第6期 】